Data measured from a high-order complex system can be difficult to analyze. A convenient tool to store such data is in the form of a tensor, or d-way array. Each entry of the array describes the value obtained across the d independent parameters. Often, the dependencies between the indices is not clear, making interpretation of the data a demanding task.
Most naturally occurring datasets are formed by directly observing and measuring quantities. As a result, the underlying or driving processes are usually unknown. We call such variables hidden or latent.
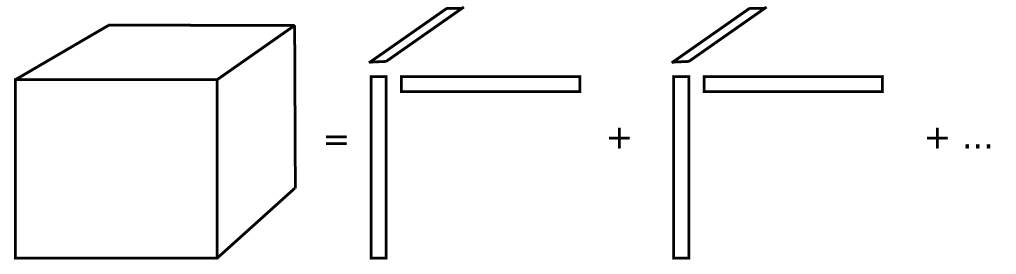
Tensor factorizations are higher-order analogs to matrix factorizations. The main goal of all tensor factorizations is to decompose the tensor into simpler objects, such as sums special products of matrices. These atomized, simple building blocks often reflect the hidden processes that went into deriving the data.