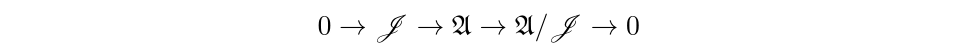
Operator Algebras Generated by Left Invertibles

Operator algebras generated by partial isometries and their adjoints form the basis for some of the most well studied classes of C*-algebras. The Toeplitz algebra is a classic example. The generator $M_z$ on the Hardy space $H^2(\mathbb{T})$ is isometric, and hence, left invertible. Motivated by questions from linear equations in Hilbert spaces (frame theory), we wish to understand particular types of operator algebras generated by left invertible operators.

In this talk, we investigate the norm closed operator algebra generated by a single left invertible operator $T$ in $\mathscr{B}(\mathscr{H})$ with a canonical left inverse (the Moore-Penrose inverse). This algebra, has rich operator algebraic structure that mimics the Toeplitz algebra. We are particularly interested in a class of left invertible operators we call \textit{analytic}. The adjoints of analytic left invertible operators are Cowen-Dogulas, an important class of operators that serve as a bridge between operator theory and complex geometry. Consequently, we can represent $T$ as $M_z$ on a reproducing kernel Hilbert space of analytic functions. Using tools of Cowen-Douglas theory, we reduce the challenge of classifying these algebras into more tractable geometric problems.