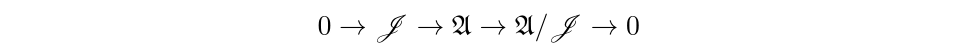
Operator Algebras Generated by Left Invertibles

Operator algebras generated by partial isometries and their adjoints form the basis for some of the most well studied classes of C*-algebras. Representations of such algebras encode the dynamics of orthonormal sets in a Hilbert space. We instigate a research program on concrete operator algebras that model the dynamics of Hilbert space frames.

The primary object of this thesis is the norm-closed operator algebra generated by a left invertible T together with its Moore-Penrose inverse. Of particular interest is when T satisfies a nondegeneracy condition called analytic. We show that T is analytic if and only if its adjoint belongs to an important class of operators called Cowen-Douglas. When the Fredholm index of T is -1, the algebra contains the compact operators, and any two such algebras are boundedly isomorphic if and only if they are similar. A classification of these algebras by K-theoritc means is then acquired.